
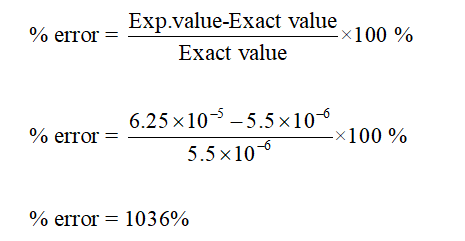
When you perform experiments, there’s always the possibility of getting a value which is either lesser or greater than the true value because of experimental or human errors. Another way you can acquire this value when your observed value is twice as large as the true value. In other words, a percent error of more than 100 is entirely possible. Generally, this occurs when you take the measurement of a quantity that’s small on average but has a distribution that’s wide and has a small number of measurements. The percent error can become over 100 if the fraction on the right is more than 1 and this is a possibility. The relativity of this value is what you take as the standard error. A value of a given quantity “x” you acquired from your experiment is the approximation of an average “x” of a specific number of “n” measurements. The short answer to this is – yes, it can be. Percent error then refers to determining how possible values may differ from the “true value” because of any device limitations. This is typically a function of the device’s construction and how it’s used, unlike accuracy which is often related to the device’s calibration. On the other hand, precision refers to the consistency of the device in delivering the same value for a specific measurement over and over again. You can calculate the percent error as the range of deviation of a certain measurement from the best and most recent fixed metric point. However, these measurements cannot change the measurement error which is inherent. Several measurements may help improve the statistic accuracy of a measurement. They are what they are and you can only improve them when you improve the device or equipment. In measurement designs, both precision and accuracy are inherent. But this doesn’t apply to both precision and accuracy. There’s only the individual’s judgment on whether or not he can make use of the data he acquired. Statisticians and scientists both say that there’s no upper limit when it comes to percent error. To make sense of this measurement, you have to take other factors into consideration too.Īlong with the percent error, the other factors are precision and accuracy. The utilization of any value with a high percent error in measurement depends on your own judgment. Some say that the percentage error can never be too high as long as you perform the calculation correctly. In most schools, instructors may accept a percentage error of 5%. But in other cases, an error as small as 1% is already too high. Sometimes, the measurement might be too difficult to take that you may consider an error of 10% or more acceptable. How acceptable the percentage error depends on the application. After performing the calculation, you can check the accuracy of your answer using the percent error calculator. So for our example, the percent error or the relative error is 4.082%.To do this, divide 14 m/s by the true value. Then you can continue with the formula in order to get the percent error. The value you acquired is the absolute error.With both values, you can start solving for the percent error using the percent error formula:.Here, let’s assume that the value you acquired was 329 m/s. Then take your own measurement based on your observation.For this example, let’s use the speed of sound in the air at a temperature of 20☌ which is 343 m/s. Go online and find out the real value of the speed of sound.To solve for the percent error using this example, here are some steps: For instance, let’s say that you want to solve for the relative error between your observed value and the true value of the speed of sound.
Percent error chemistry calculator manual#
You may also find this value by performing a manual calculation using the percent error equation which is:įor you to understand the concept of percent error better, let’s look at an example. If you want to check the percent error, you can use the relative error calculator or the absolute error calculator. However, your observed measurement may deviate slightly from the actual gravitational acceleration. In this case, you may try performing the experiment several times in order to get a good estimate of the actual acceleration time. For instance, you can try to solve for the gravitational acceleration by measuring how much time a free-falling object would take from top to bottom from a certain height.

Often, when you try to come up with an estimated value of a specific quantity, you do this by making several measurements repeatedly.


 0 kommentar(er)
0 kommentar(er)
